五月色婷婷 “克莱因瓶”有多诡异？为什么科学家穷其一世也无法造出？

我们正常看东西，王人可爱用维度来分辩，啥平面的、立体的、多面的，一眼就能瞧出个无意。那说到三维和四维的玩意儿，区别在哪儿呢？今儿个就来聊聊阿谁据说中的“克莱因瓶”，据说这玩意儿邪乎得很五月色婷婷，科学家们连续一辈子王人整不出来，今儿个咱就来瞧瞧这玩意儿到底有多神奇。

“克莱因瓶”这玩意儿到底有多邪乎？为啥科学家们连续一辈子王人整不出来？

四维空间，说白了便是阿谁据说中的“克莱因瓶”，揣度许多东谈主王人不太显着这玩意儿是啥。精真金不怕火来说，你不错念念象成从我们这三维空间去看四维空间，就像我们正常看二维平面图雷同。其实四维空间说白了便是三维空间从不同角度看的恶果，这样说是不是显着点了？

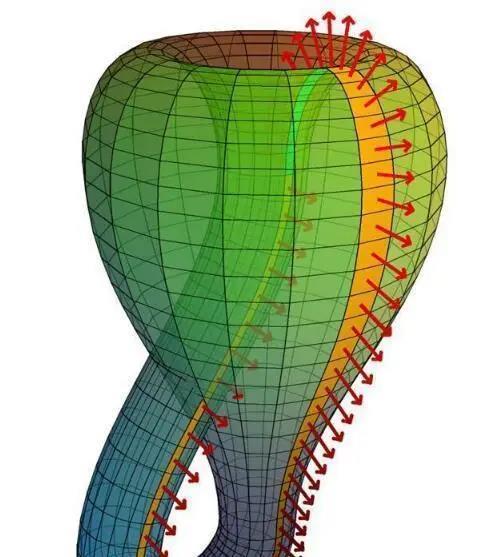
哥要搞蝴蝶谷

不外在四维寰宇里，克莱因瓶的瓶颈可不是平直穿过瓶身和瓶底连一块儿的，而是绕着瓶身平直通到瓶底的瓶口，要津是这个瓶口根本儿就不在我们这三维空间里，而是在四维空间里，通过四维空间和瓶底连在沿路，是以通盘这个词克莱因瓶就能从瓶底一齐通到瓶口，中间啥隐私王人莫得。

这旨趣其实和阿谁啥莫比乌斯环差未几，莫比乌斯环便是两面王人有的平面，转个180度就能连一块儿，上头的东西就能一直跑下去，无谓绕圈圈。莫比乌斯环在二维寰宇看着是误会的，但在我们三维寰宇里就合理得很，因为这种误会，上头的东西就能一直跑下去，无谓掉头，也便是说，二维寰宇里的东西在二维寰宇里不好整，但在三维寰宇里就能节略解决，何况透顶合适谋划条件。

那么问题来了五月色婷婷，像克莱因瓶这种四维空间的玩意儿，我们这些三维空间的东谈主类能造出来吗？能不成通过克莱因瓶这玩意儿来了解着实的四维空间到底是啥样的，从而搞显着弦表面里说的天地九维空间加一维时分到底有啥意旨？